皆さん、こんにちは。リンスタ広報担当の大橋です！前回に引き続き、高校受験数学の入試問題分析をお送りいたします。今回は、「大阪府B問題」です。それでは、いってみましょう。

大阪府では、国語、数学、英語の問題パターンがA問題、B問題、C問題の3つに分かれています。各高校が入試問題をこの3つのなかから採択をします。科目ごとに異なる問題を採択することも可能です。今回は、採択高校が一番多かったB問題を解説します。B問題は解答のみを答える形式が基本ですが、特徴的な問題として「途中式を含めた考え方の説明」と「図形の証明」が記述形式で1問ずつ出題されます。問題構成は、1⃣計算問題(15点)、2⃣小問集合(29点）、3⃣関数(16点)、4⃣図形の各分野(30点)です。図形分野では平面図形、立体図形ともに出題され配点が多いことが特徴です。また、他の大問に比べ、正答率が低いことから、入試において「差」のつく問題となっています。

さて、今回の「差」がつく1問は、大問4〔１〕です。この問題は、入試でよく問われる要素が詰め込まれていますので、「平面図形の手の動かし方」を学びましょう。

題：図Ⅰにおいて、四角形ABCDは1辺の長さが9 cmの正方形である。△EFCは∠EFC = 90°の直角三角形であり、EF > FCである。Fは、辺A上にあってA、Bと異なる。Gは、辺EFと辺ADの交点である。辺ECは、辺ADと交わっている。Hは、Gを通り辺FCに平行な直線と辺ECの交点である。Iは、直線GHと辺DCの交点である。次の問いに答えなさい。
(1) △GAF ∽ △FBCであることを証明しなさい。
(2) FB = 3 cm、EF : FC = 5 : 3であるとき、
①線分GFの長さを求めなさい。
②線分HIの長さを求めなさい。

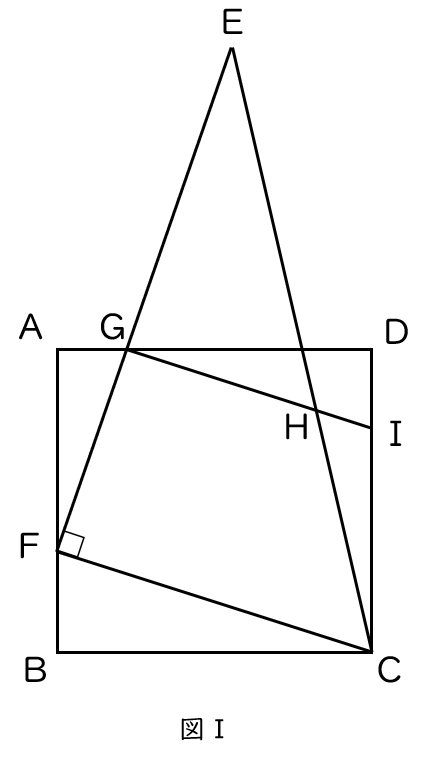
まずは、(1)。相似の証明！

まずは、問題文の情報を図に書き入れましょう。このとき、計算すれば求まる長さや、同じ大きさの角も書き入れましょう。今回であれば、GI ∥ FCなので、平行線の同位角が等しいことから∠EGI　= ∠EFC = 90°とわかります。すぐに書き入れましょう。直角三角形もありますね。ここで、やってほしいこと。それは、『直角三角形を見つけたら、角度を記号であらわす。』です。今回の場合、∠AFGの大きさを〇、∠AGFの大きさを×としましょう。∠GAF = 90°ですから、〇+× = 90°になりますね。ここで、点Fに注目してみましょう。〇と90°がありますね。これを用いると、∠BFCを記号であらわすことができそうです。∠AFG(〇)と∠BFCの和は、∠GFC = 90°であることから、90°です。∠AFGは〇ですから、∠BFCは×となります。もう一度、△GAFと△FBCに目をうつすと同じ大きさの角が２つ見つかります。これを上手に書ければ、(1)の証明はできそうです。三段論法を使用すると、書きやすいでしょう。

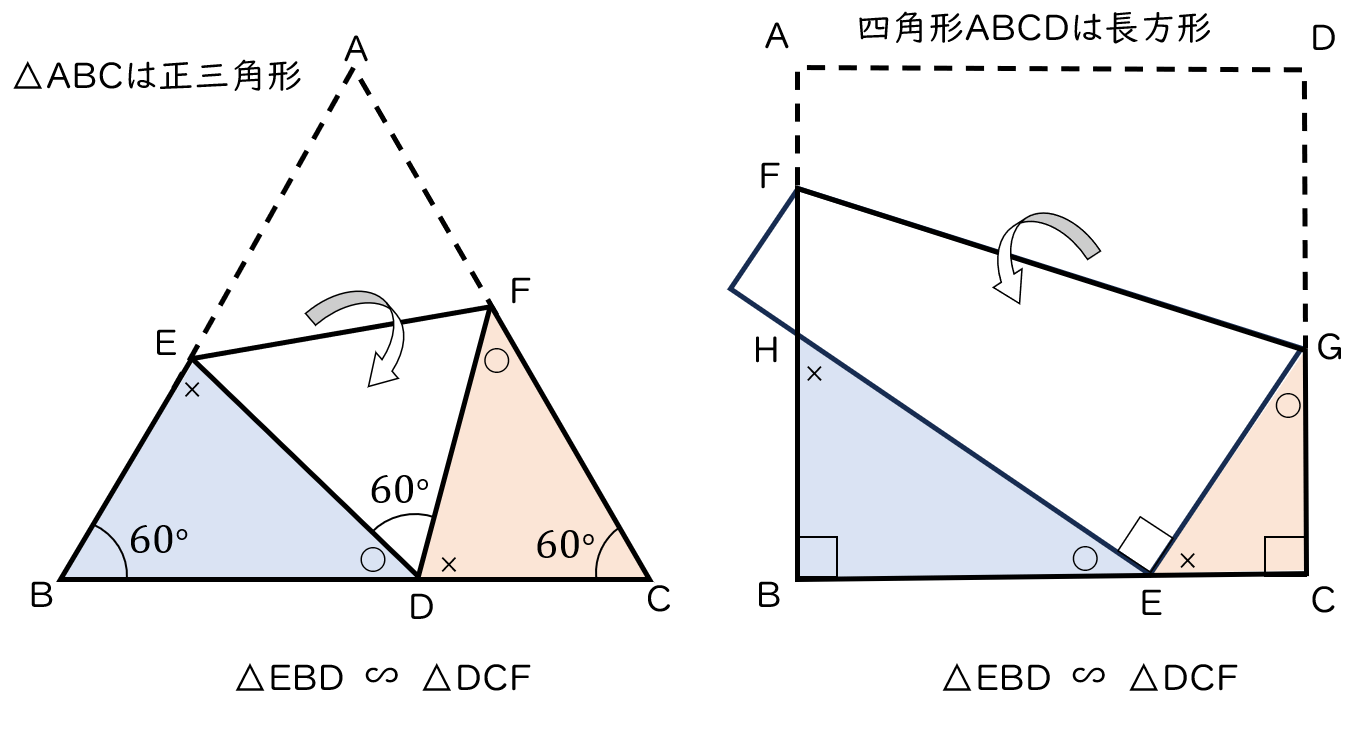
「一直線上に同一角度が3つは、相似！」

実は、この相似の形よく出題されるんです。キーワードは、『一直線上に同一角度が3つ並ぶときは、相似が登場』です。今回は、辺ABに直角が3つ並んでいますね。よく出てくるパターンは直角ですが、他の角度でも成り立ちます。証明は、以下の通りです。先ほどと同様に書いてみました。

相似の証明は、できましたね。それでは、この「一直線上に同一角度が3つ並ぶときは、相似が登場」の具体例です。長方形(正方形含む)や、正三角形の「折り返し」でよく登場します。

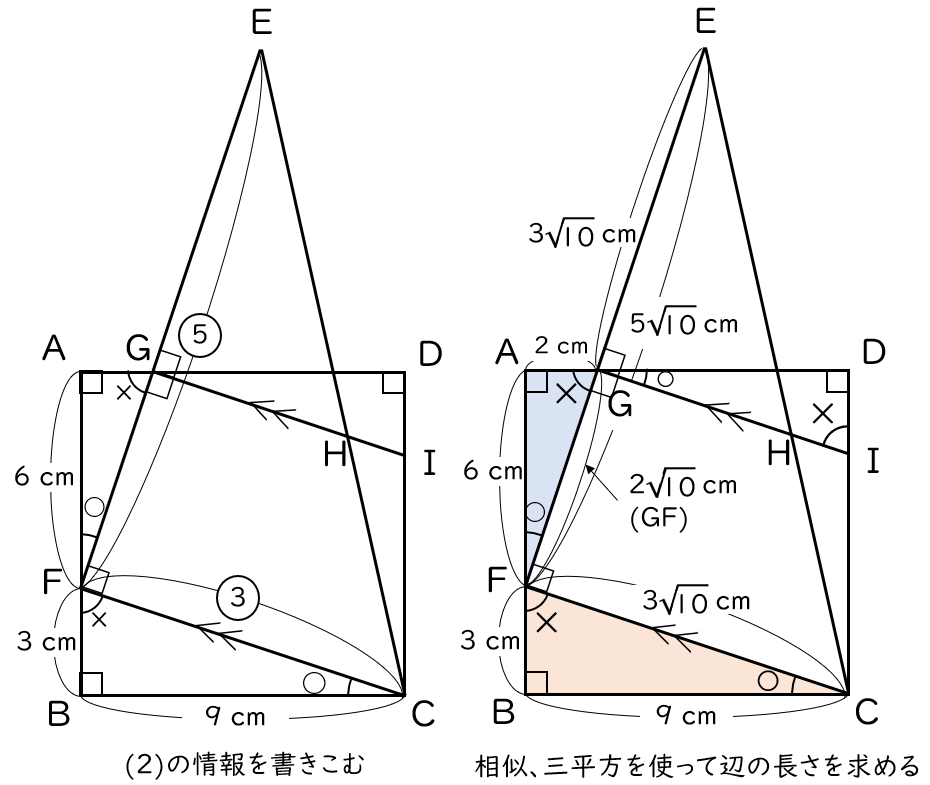
いざ、ラスボス。小さなことの積み重ね。

さぁ、(2)も頑張っていきましょう。(1)で相似を証明したので、それを用いて(2)を解くのだと想像ができます。(2)では、新たに辺の長さが与えられました。まずは、新情報を書き入れましょう。また、(1)で△GAFと△FBCが相似であると証明できたことで、長さを求められる辺がありますね！相似な図形は、「対応する辺の比が等しく」、「対応する角の大きさが等しい。」です。対応する辺の比を考えると、AE : BC = AG : BFとなります。AF = 6 cm、BC = 9 cm、BF = 3 cmとわかっているので、AGの長さが求まります。また、直角三角形ということで、アレが使えますね。そう、三平方の定理！この2つの三角形の3辺の長さは、すべて求まるはずです。ということで、書き入れると図のようになり、線分GFはこれで求まります。これで①は解決しましたね。さぁ、②も解いていきましょう。EF : FC = 5 : 3を用いると、辺EFの長さも求まります。書き入れた図をよく見ると、△GAFと△FBCと相似な三角形がもう一つあります。〇や×をきちんと書き入れていればみつかるはず！∠FGI = 90°に注目すると、、、そう、△IDGですね。△IDGの辺の長さも書き入れましょう。△GAFと対応する辺の比を考えれば出すことができますね。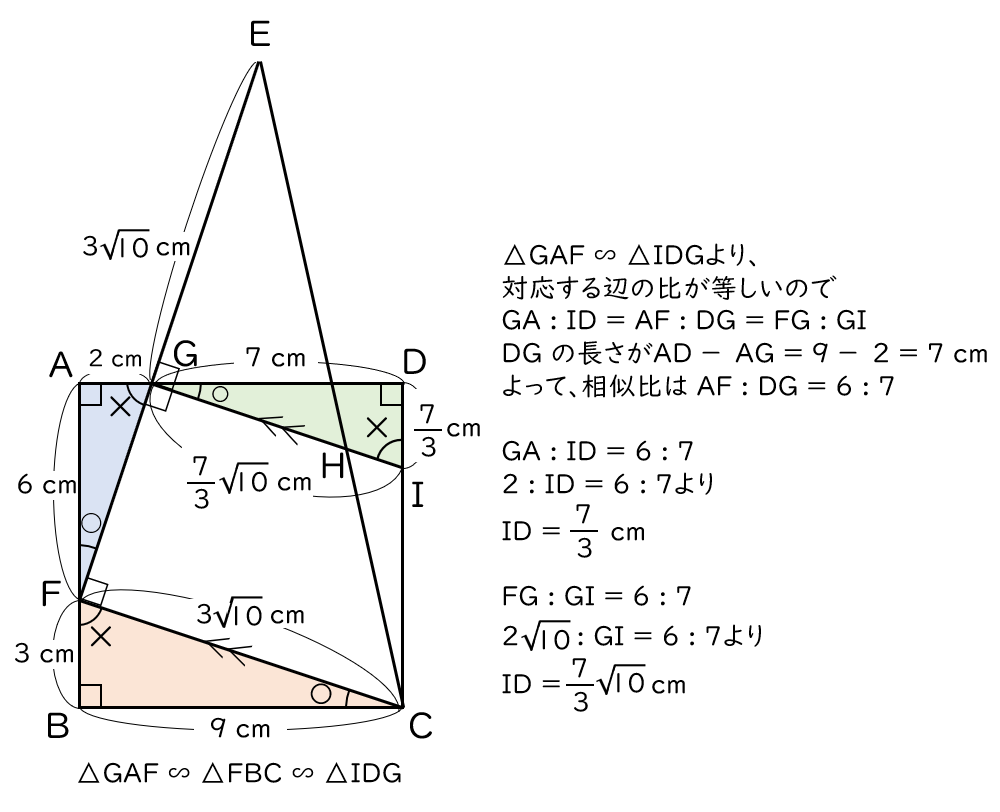

ここで問題をもう一度確認しておきましょう。問題で問われている長さは辺HIです。いま、辺GIは求まりました。辺HIを求めるためには、どこの長さが必要でしょうか。辺GHです。辺GHは、△EGHの一辺です。辺EGの長さは、辺EFと辺GFの長さがわかっているので求まります。∠EGH = ∠EFC = 90°、∠Eが共通なので、△EFCと△EGHは相似といえます。対応する辺の比は等しいですから、EF : EG = FC : GHが成り立ちます。あとは、比の計算をすると、辺GHが求まり、辺HIが求まります。

さぁ、今回は相似も三平方の定理もふんだんに使った問題でしたね。定番の手の動かし方をきちんとマスターしましょう。最後にまとめておきますね。

「明るく」「楽しく」「元気よく」
頭を使って数学を解きましょう！

それでは、また次回お会いしましょう！