皆さん、こんにちは。リンスタの広報担当大橋です！担当教科は高校受験の花形である数学です！EIKOH LiNKSTUDYはオンライン指導のメリットを活かし、全国各地から多くの生徒に受講いただいています。こちらのブログでは、我々の問題研究の一部として、47都道府県の問題分析をお伝えします。初回は、東京都共通問題！それでは、いってみましょう！

東京都共通問題は、マークシートでの解答が基本となります。ただし、特徴的な問題として、「文字を用いた説明」と「図形の証明」が記述形式で1問ずつ出題されます。また、大問構成や配点は固定されており、1⃣小問集合、2⃣文字式、3⃣関数、4⃣平面図形、5⃣立体図形の各分野より出題されます。100点満点のうち、1⃣の小問集合が46点と大きな割合を占めていることが一つの特徴と言えるでしょう。また、中でも計算問題が46点中6問30点を占めています。大問1は、基礎的な問題が多く、令和4年で68.3%、令和5年で76.5%と、高い正答率となっています。逆に受験生を苦しめるのは、大問5空間図形と言えます。正答率は令和4年で15.6%、令和5年で7.8%となっており、入試において「差」のつく問題となっています。

さて、今回の「差」がつく1問は、大問5〔問2〕です。空間図形に対して、苦手意識がある人も多いのではないでしょうか。空間図形は、図形の見方によって難度が左右されます。正しい図形の見方ができれば、楽になる問題も多くあります。この解説では、様々な図形の見方を伝えていきます。

問題：大問5〔問2〕
立体ABC－DEFは，AB = AD = 6 cm，AC = BC = 5 cm，∠BAD = ∠CAD = 90°の三角柱である。辺CF上にあり，頂点C，頂点Fのいずれにも一致しない点をPとする。頂点Aと点P，頂点Bと点P，頂点Dと点P，頂点Eと点Pをそれぞれ結んだ場合を考える。立体P-ADEBの体積を求めなさい。

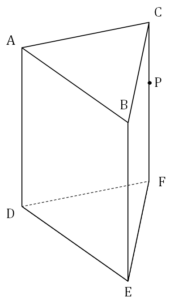
ということで、解説していきます。今回のキーワードは、『いつもの形になおす』。この1文、よく覚えておいてくださいね。数学ではとても大切な考え方です。

問題解く前の下準備

最初にやるべきことは、問題をよく読み、情報を図にうつすことです。数学では、問題文の情報を組み合わせることで、新たに見えてくる情報があります。辺の長さや、角度の大きさをうつしたものが、下の図です。この図から、△ABCが二等辺三角形であり、四角形ADEBが正方形とわかります。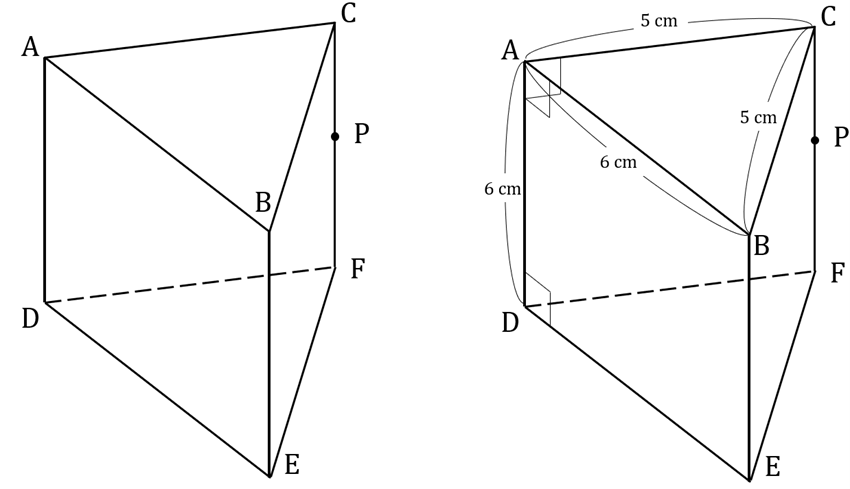

この立体はなにもの？

今回は、立体P-ADEBの体積を求める問題ですので、問題文に従って立体P－ADEBを三角柱の中に作ります。図のようなオレンジ色の立体になります。ここで、立体の特徴をつかむために、立体の面の形や、辺の数をよく観察しましょう。面の形に注目すると、正方形1つに三角形が4つついています。この立体の名前は、何でしょうか。そう、「四角錐」ですね。この四角錐の体積を求めたいわけですが、方針が思いつくでしょうか。ここで、今日のキーワード「いつもの形になおす。」通常、四角錐をどのような向きで目にするでしょうか。よく思い出してみましょう。四角形が地面にくっついた四角錐をよく目にするかと思います。大抵の場合、〇〇錐の〇〇は、底面として、地面にくっついています。これが「いつもの形」です。四角形ABEDを地面に置いてみると図のようになります。

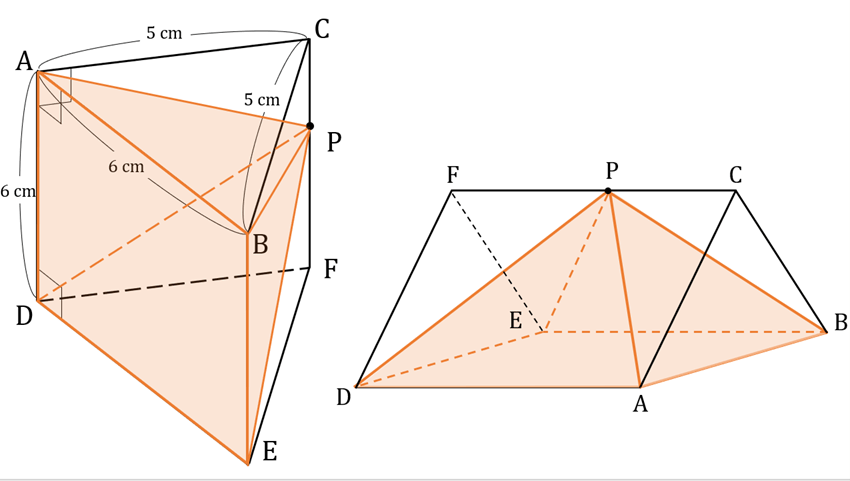ちなみに、問題文から四角錐であることを読み取りことができます。「―」を用いてP－ADEBのように表す場合、「―」の左側が頂点を、右側が底面を表します。立体P－ADEBとあるので、Pが頂点で、四角形ADEBが底面です。

体積を求めよう！

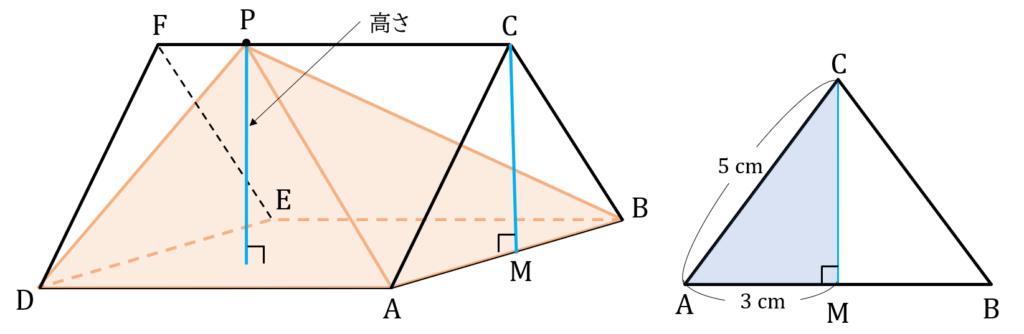
体積を求めたいので、底面と高さが必要です。底面は四角形ADEBですので、高さを引いてみましょう。高さは、Pから四角形ADEBに垂線ですね。立体図形で困ったときに使える考え方を紹介します。「真〇からみる」です。真〇とは真上、真横のことです。今回は、真横からみてみましょう。真横からみると、Pから下した垂線の長さと、CからABに下した垂線の長さが同じです。△ABCは、AB = BCの二等辺三角形ですので、Cから下した垂線は、底辺のちょうど真ん中に来ます。交点をMとします。△CAMは、直角三角形です。直角三角形の1辺を求めるために、三平方の定理を使いましょう。三平方の定理について深く知りたい人は、河野先生の記事を要チェックです。三平方の定理を使うときは、辺の比から確認しましょう。なんと、今回は「3：4：5」の直角三角形ですね！ということで、平方根の計算をせずにCMの長さは4 cmと求められます。これは、今回求めたい立体の高さと長さですので、高さが4 cmと求まります。

最後に，体積の公式を使って体積求めちゃいましょう。

に各々の数字を代入すると，48 ㎤と求まります。

今回の問題、いかがでしょうか。立体図形は「見方」を変えることで、問題が解きやすくなります。今回、伝えたものは、立体図形の問題に取り組むとき、いつでも使える考え方です。

「明るく」「楽しく」「元気よく」
頭を使って数学を解きましょう！

それでは、また次回お会いしましょう！