円周率のいろいろ

みなさん、こんにちは。
リンスタ数学担当 河野 です。
ちょっとリーマン予想の証明に挑んでいたら、ひさかたぶりの更新になってしまいました。
全く以てボクの能力では無理なので、また改めてブログ、再開していきますね！

さて、今日は表題のとおり『円周率』について書こうと思います。

きっかけは東京都渋谷区にある青山学院高等部の2023年度入試問題。それは、以下のような図を用いて円周率の範囲を特定せよ、という問題でした。

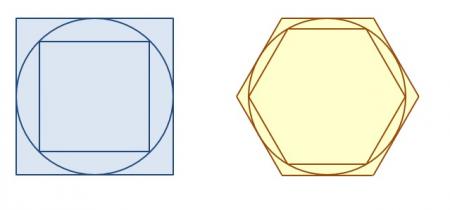
円の直径を１とすると、中１以上の皆さんはご存知のとおり、円周の長さは「π（パイ）」。

π＝3.14159 26535 89793 23846… と続く、「円周率」と呼ばれる無限小数ですね。
図形から πは円の内側に書かれた正方形や正六角形の周の長さより長く、外側に書かれたものより長いということになりますから、そこから範囲が特定できるね、という問題でした。同様の方針で解答できる問題が、2003年に東京大学で出題されているのも有名です。
（「円周率が3.05よりも大きいことを証明せよ。」という問題でした。）

実はこの方法、紀元前2000年頃（つまり今から4000年以上前）には知られていたと言われています。当時は中学入試 算数で時折見かける「22/7（＝3.142857…）」などが用いられていたとのこと。東大 入試問題レベルの概数についても、紀元前3世紀頃（前回ブログのユークリッドさんと同じころですね）にアルキメデスによって発見されていたそうです。

ちなみにその後、紆余曲折を経ての現在、円周率は何桁まで計算されているかご存知ですか？
このブログを書いている2023年3月現在では、なんと『100兆桁』。
そしてこれを達成したのは 岩尾エマはるかさん という、日本の開発者なんです！

「そんなに円周率を計算して、何の意味があるの？」って思います？？
これは大きな意味があります。
というのもこの計算、なんと 157日23時間31分 もかかったそうで…。
昔から知られる円周率を、大量のデータを扱って計算することは、「コンピューターの性能を表す尺度」になるんですね。

円周率は書いているとキリがないほど興味深い数なので、残りはざっと箇条書きで…

【ランダム性】
円周率を無限に計算すると、０から９までの数字が均等に出てくると言われています。（本当にそうなのかは、証明されていません。）

【記念日】
3月14日：円周率の日・数学の日（πが永遠に続く数のため、この日を結婚記念日にする人もいるんですって。）
7月22日：記事中に登場した近似値「22/7」から、円周率近似値の日とされています。
※どっちも学校が休みになることはないのでご注意！

【円周率の暗唱】
現在のギネス世界記録はインドの方が打ち立てた7万桁。
なお、日本人の 原口證さん は2006年に10万桁の暗記を達成しギネスへ申請中とのことですが、現時点では正式認定されていません。
（ちなみに暗唱には16時間30分もかかったんですって… すごいですね…。）

前回の記事はこちら